Distribution Sampelr
Introduction
In this part, comparsion between actual sampler results and standard distribution is implemented, and all distribution sampler demo are exhibited as well.
Code can be found in pydpm/example/Sampler_Demo.py
The last default param ‘times=1' are skipped over.
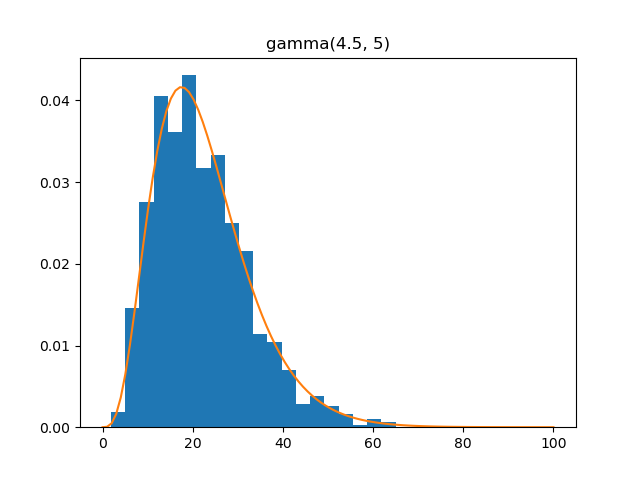
Gamma
Demo
from pydpm._sampler import Basic_Sampler
import scipy.stats as stats
output = sampler.gamma(np.ones(1000)*4.5, 5)
plt.figure()
plt.hist(output, bins=20, density=True)
plt.plot(np.linspace(0, 100, 100), stats.gamma.pdf(np.linspace(0, 100, 100), 4.5, scale=5))
Plot
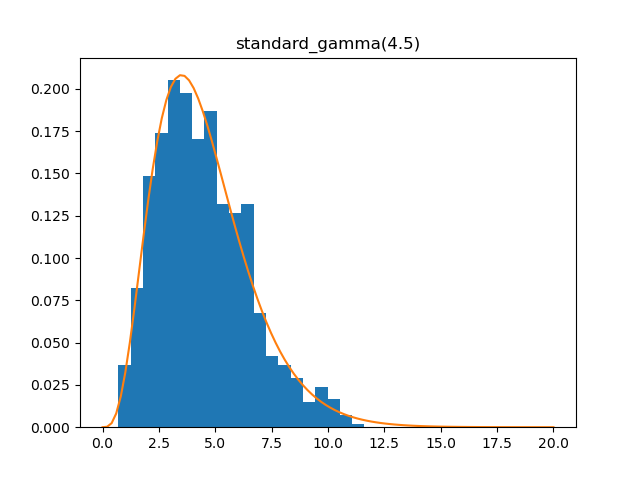
Standard gamma
Demo
from pydpm._sampler import Basic_Sampler
import scipy.stats as stats
output = sampler.standard_gamma(np.ones(1000)*4.5)
plt.figure()
plt.hist(output, bins=20, density=True)
plt.plot(np.linspace(0, 20, 100), stats.gamma.pdf(np.linspace(0, 20, 100), 4.5))
Plot
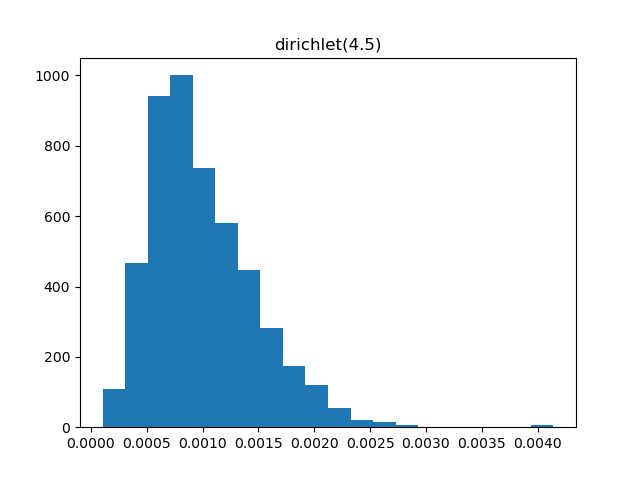
Dirichlet
Demo
from pydpm._sampler import Basic_Sampler
import scipy.stats as stats
output = sampler.dirichlet(np.ones(1000)*4.5)
plt.figure()
plt.hist(output, bins=20, density=True)
Plot
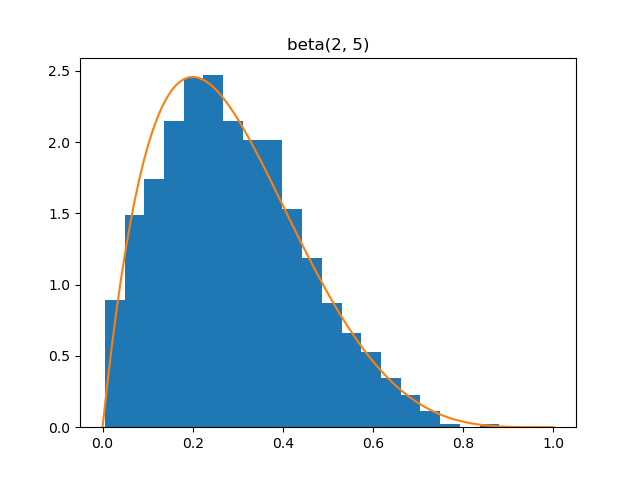
Beta
Demo
from pydpm._sampler import Basic_Sampler
import scipy.stats as stats
output = sampler.beta(np.ones(1000)*2, 5)
plt.figure()
plt.hist(output, bins=20, density=True)
plt.plot(np.linspace(0, 1, 100), stats.beta.pdf(np.linspace(0, 1, 100), 2, 5))
Plot
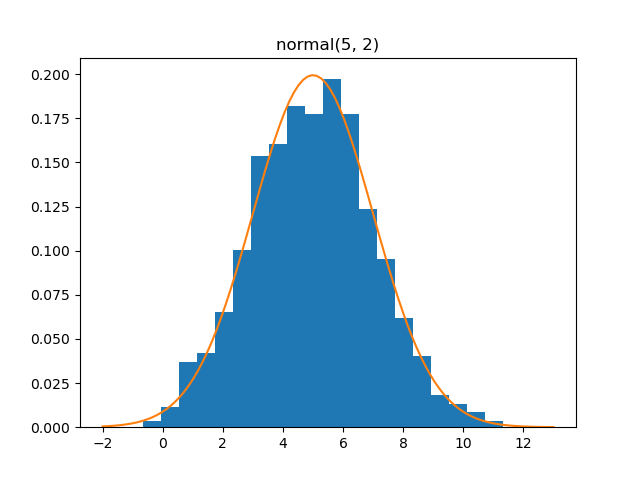
Normal
Demo
from pydpm._sampler import Basic_Sampler
import scipy.stats as stats
output = sampler.normal(np.ones(1000)*5, np.ones(1000)*2)
plt.figure()
plt.hist(output, bins=20, density=True)
plt.plot(np.linspace(-2, 13, 100), stats.norm.pdf(np.linspace(-2, 13, 100), 5, scale=2))
Plot
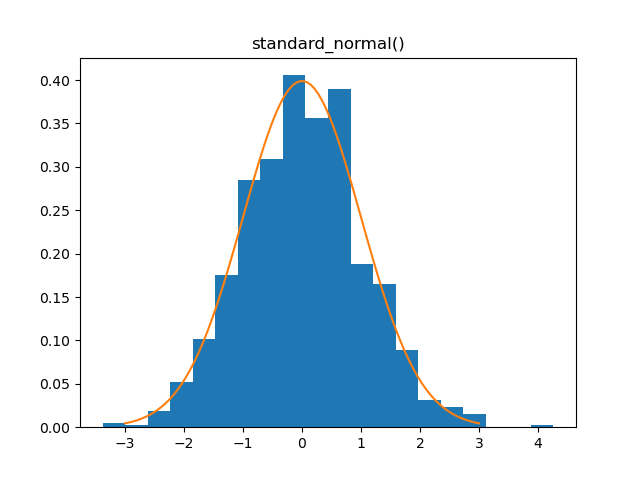
Standard Normal
Demo
from pydpm._sampler import Basic_Sampler
import scipy.stats as stats
output = sampler.standard_normal(1000)
plt.figure()
plt.hist(output, bins=20, density=True)
plt.plot(np.linspace(-3, 3, 100), stats.norm.pdf(np.linspace(-3, 3, 100)))
Plot
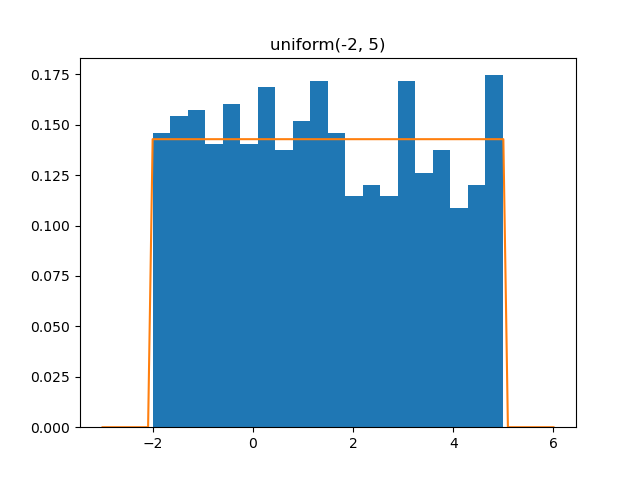
Uniform
Demo
from pydpm._sampler import Basic_Sampler
import scipy.stats as stats
output = sampler.uniform(np.ones(1000)*(-2), np.ones(1000)*5)
plt.figure()
plt.hist(output, bins=20, density=True)
plt.plot(np.linspace(-3, 6, 100), stats.uniform.pdf(np.linspace(-3, 6, 100), -2, 7))
Plot
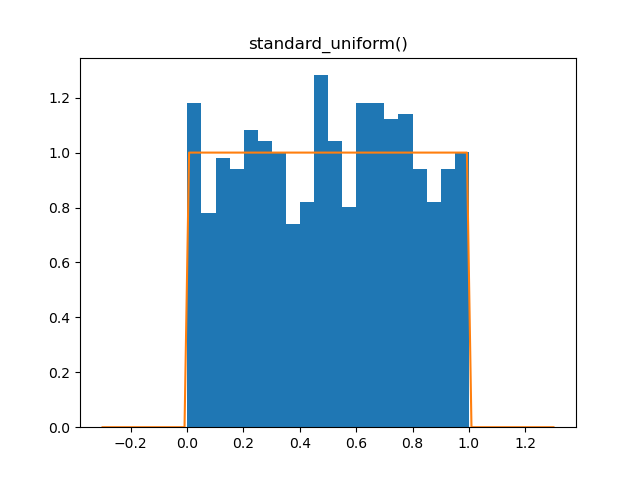
Standard Uniform
Demo
from pydpm._sampler import Basic_Sampler
import scipy.stats as stats
output = sampler.standard_uniform(1000)
plt.figure()
plt.hist(output, bins=20, density=True)
plt.plot(np.linspace(-0.3, 1.3, 100), stats.uniform.pdf(np.linspace(-0.3, 1.3, 100)))
Plot
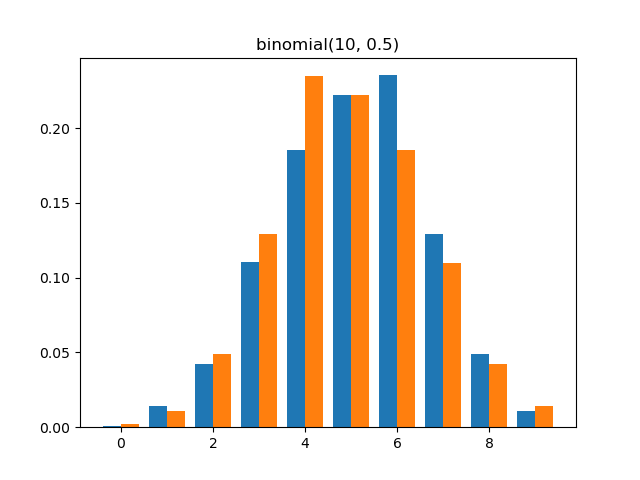
Binomial
Demo
from pydpm._sampler import Basic_Sampler
import scipy.stats as stats
output = sampler.binomial(np.ones(1000)*10, np.ones(1000)*0.5)
plt.figure()
plt.hist(output, bins=np.max(output)-np.min(output), density=True, range=(np.min(output)-0.5, np.max(output)-0.5))
Plot
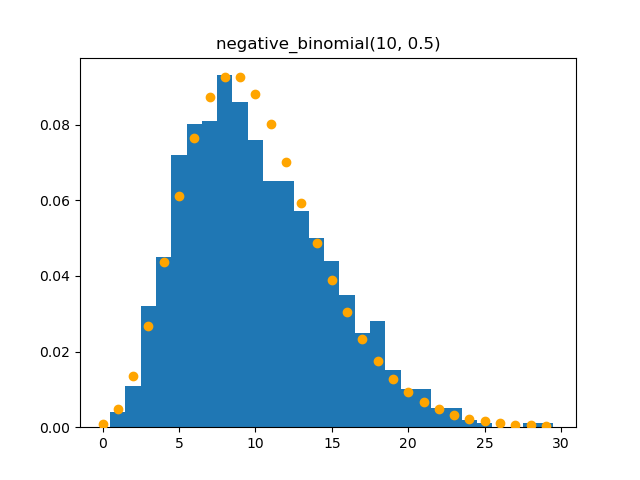
Negative Binomial
Demo
from pydpm._sampler import Basic_Sampler
import scipy.stats as stats
output = sampler.negative_binomial(np.ones(1000)*10, 0.5)
plt.figure()
plt.hist(output, bins=np.max(output)-np.min(output), density=True, range=(np.min(output)-0.5, np.max(output)-0.5))
plt.scatter(np.arange(30), stats.nbinom._pmf(np.arange(30), 10, 0.5), c='orange', zorder=10)
Plot
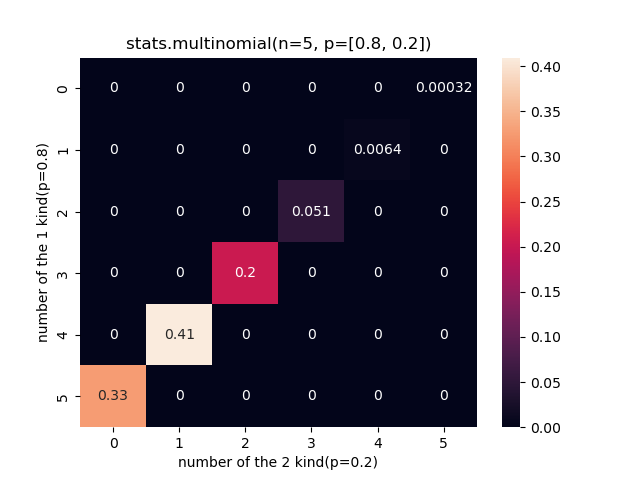
Multinomial
Demo
from pydpm._sampler import Basic_Sampler
import scipy.stats as stats
output = sampler.multinomial(5, [0.8, 0.2], 1000)
plt.figure()
plt.hist(output[0], bins=15, density=True)
plt.title('multinomial(5, [0.8, 0.2])')
plt.show()
a = np.array([np.array([[i] * 6 for i in range(6)]).reshape(-1), np.array(list(range(6)) * 6)]).T
output = stats.multinomial(n=5, p=[0.8, 0.2]).pmf(a)
sns.heatmap(output.reshape(6, 6), annot=True)
plt.ylabel('number of the 1 kind(p=0.8)')
plt.xlabel('number of the 2 kind(p=0.2)')
plt.title('stats.multinomial(n=5, p=[0.8, 0.2])')
Plot
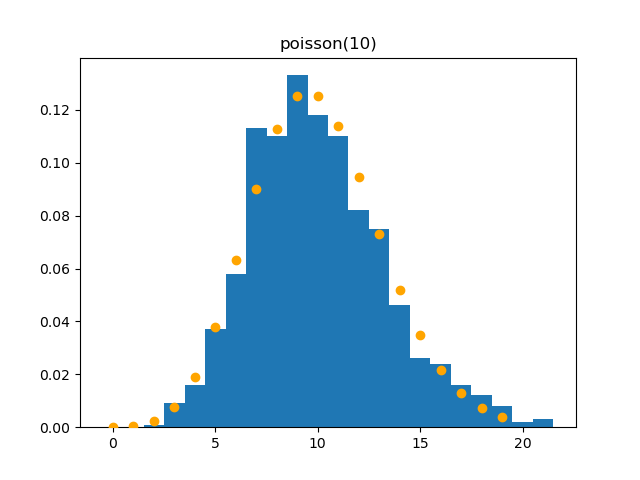
Poisson
Demo
from pydpm._sampler import Basic_Sampler
import scipy.stats as stats
output = sampler.poisson(np.ones(1000)*10)
plt.figure()
plt.hist(output, bins=22, density=True, range=(-0.5, 21.5))
plt.scatter(np.arange(20), stats.poisson.pmf(np.arange(20), 10), c='orange', zorder=10)
Plot
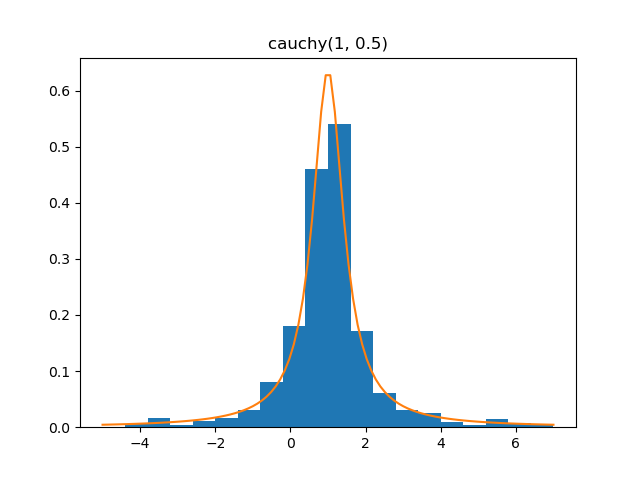
Cauchy
Demo
from pydpm._sampler import Basic_Sampler
import scipy.stats as stats
output = sampler.cauchy(np.ones(1000)*1, 0.5)
plt.figure()
plt.hist(output, bins=20, density=True, range=(-5, 7))
plt.plot(np.linspace(-5, 7, 100), stats.cauchy.pdf(np.linspace(-5, 7, 100), 1, 0.5))
Plot
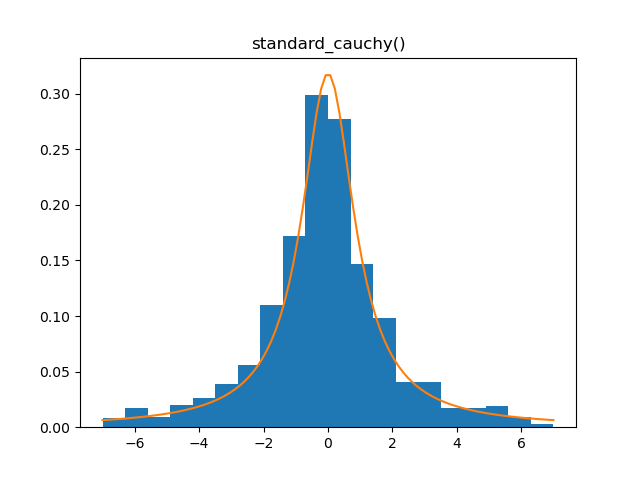
Standard Cauchy
Demo
from pydpm._sampler import Basic_Sampler
import scipy.stats as stats
output = sampler.standard_cauchy(1000)
plt.figure()
plt.hist(output, bins=20, density=True, range=(-7, 7))
plt.plot(np.linspace(-7, 7, 100), stats.cauchy.pdf(np.linspace(-7, 7, 100)))
Plot
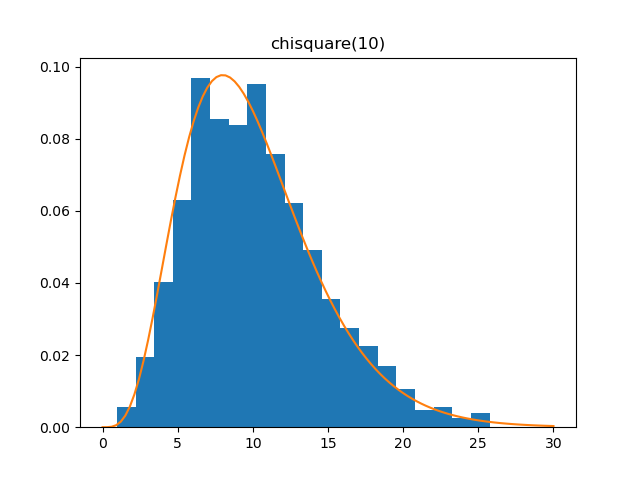
Chisquare
Demo
from pydpm._sampler import Basic_Sampler
import scipy.stats as stats
output = sampler.chisquare(np.ones(1000)*10)
plt.figure()
plt.hist(output, bins=20, density=True)
plt.plot(np.linspace(0, 30, 100), stats.chi2.pdf(np.linspace(0, 30, 100), 10))
Plot
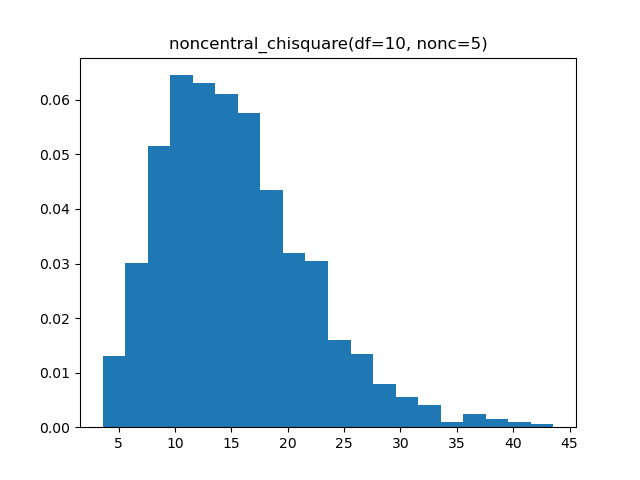
Noncentral Chisquare
Demo
from pydpm._sampler import Basic_Sampler
output = sampler.noncentral_chisquare(np.ones(1000)*10, 5)
plt.figure()
plt.hist(output, bins=20, density=True)
Plot
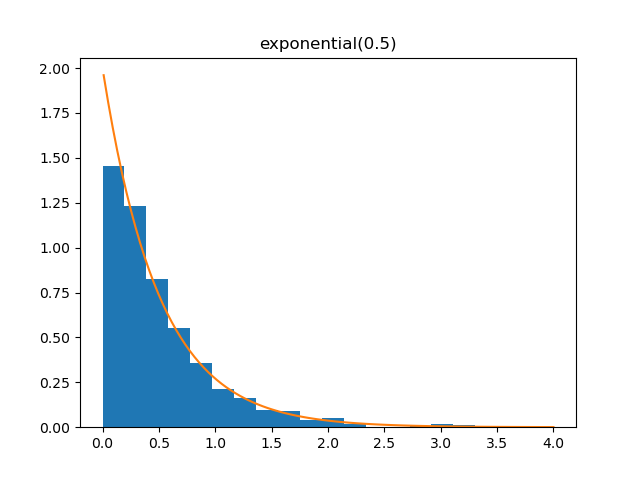
Exponential
Demo
from pydpm._sampler import Basic_Sampler
import scipy.stats as stats
lam = 0.5
output = sampler.exponential(np.ones(1000)*lam)
plt.figure()
plt.hist(output, bins=20, density=True)
plt.plot(np.linspace(0.01, 4, 100), stats.expon.pdf(np.linspace(0.01, 4, 100), scale=0.5))
Plot
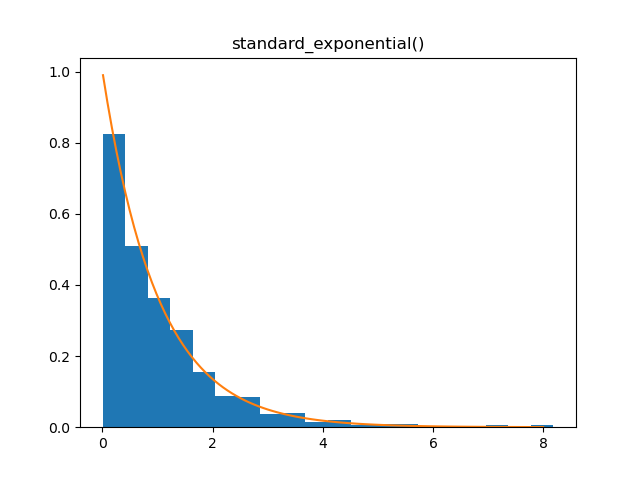
Standard Exponential
Demo
from pydpm._sampler import Basic_Sampler
import scipy.stats as stats
output = sampler.standard_exponential(1000)
plt.figure()
plt.hist(output, bins=20, density=True)
plt.plot(np.linspace(0.01, 8, 100), stats.expon.pdf(np.linspace(0.01, 8, 100)))
Plot
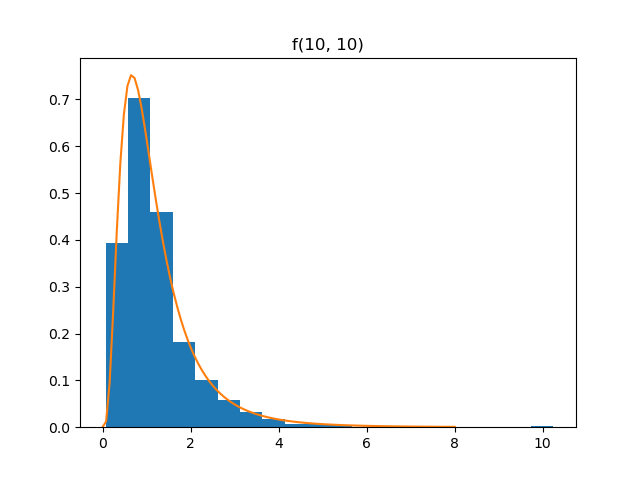
F
Demo
from pydpm._sampler import Basic_Sampler
import scipy.stats as stats
output = sampler.f(np.ones(1000)*10, 10)
plt.figure()
plt.hist(output, bins=20, density=True)
plt.plot(np.linspace(0, 8, 100), stats.f.pdf(np.linspace(0, 8, 100), 10, 10))
Plot
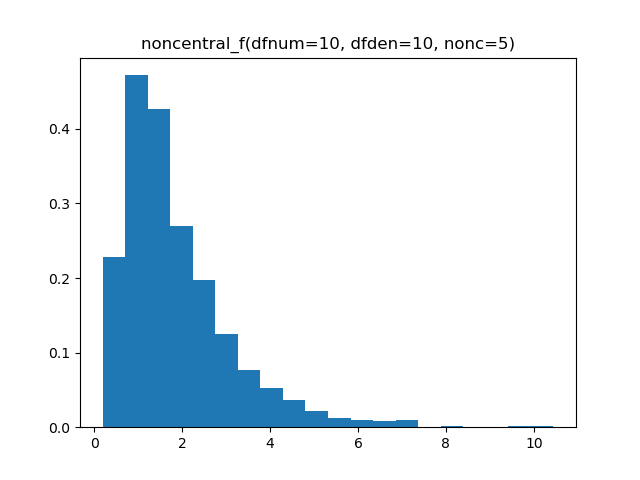
Noncentral F
Demo
from pydpm._sampler import Basic_Sampler
output = sampler.noncentral_f(np.ones(1000)*10, 10, 5)
plt.figure()
plt.hist(output, bins=20, density=True)
Plot
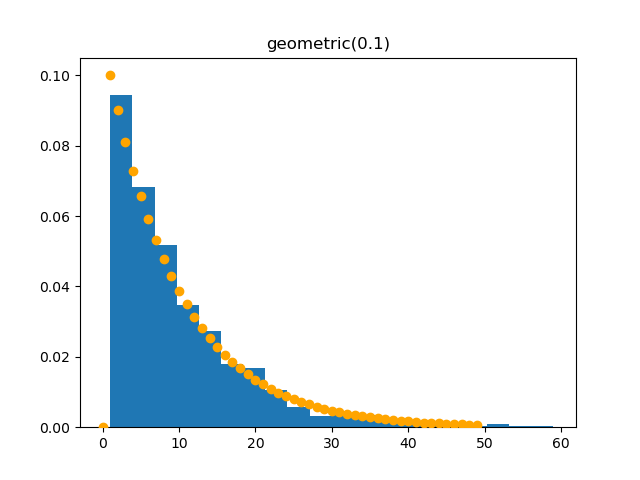
Geometric
Demo
from pydpm._sampler import Basic_Sampler
import scipy.stats as stats
output = sampler.geometric(np.ones(1000)*0.1)
plt.figure()
plt.hist(output, bins=20, density=True)
plt.scatter(np.arange(50), stats.geom.pmf(np.arange(50), p=0.1), c='orange', zorder=10)
Plot
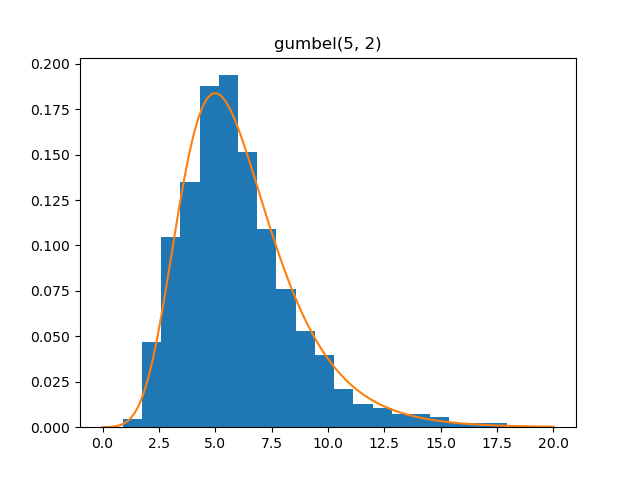
Gumbel
Demo
from pydpm._sampler import Basic_Sampler
import scipy.stats as stats
output = sampler.gumbel(np.ones(1000)*5, np.ones(1000)*2)
plt.figure()
plt.hist(output, bins=20, density=True)
plt.plot(np.linspace(0, 20, 100), stats.gumbel_r.pdf(np.linspace(0, 20, 100)+0.01, 5, scale=2))
Plot
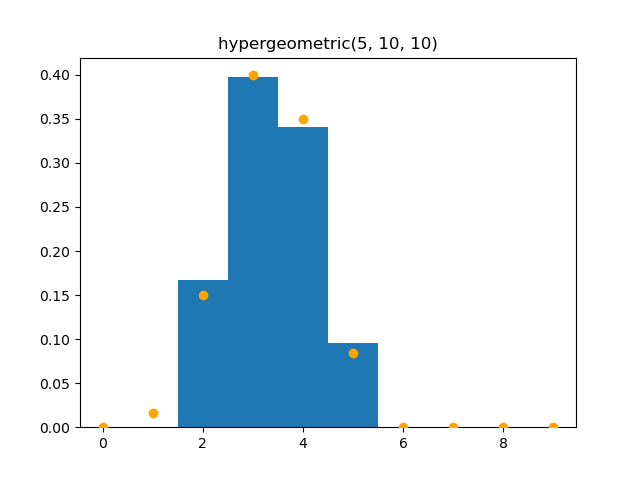
Hypergeometric
Demo
from pydpm._sampler import Basic_Sampler
import scipy.stats as stats
output = sampler.hypergeometric(np.ones(1000)*5, 10, 10)
plt.figure()
plt.hist(output, bins=np.max(output)-np.min(output), density=True, range=(np.min(output)+0.5, np.max(output)+0.5))
plt.scatter(np.arange(10), stats.hypergeom(15, 5, 10).pmf(np.arange(10)), c='orange', zorder=10) # hypergeom(M, n, N), total, I, tiems
Plot
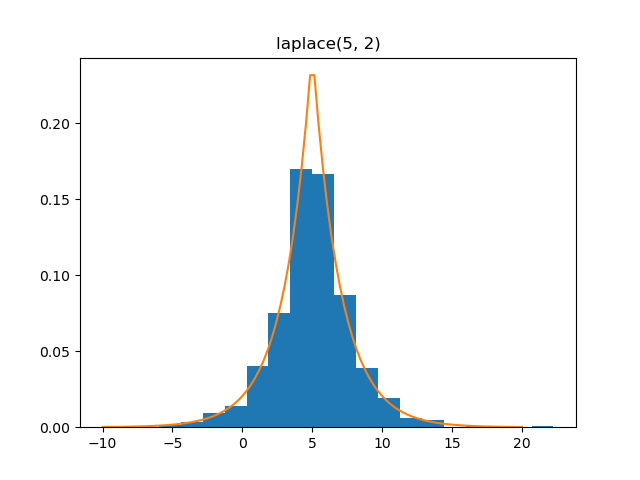
Laplace
Demo
from pydpm._sampler import Basic_Sampler
import scipy.stats as stats
output = sampler.laplace(np.ones(1000)*5, np.ones(1000)*2)
plt.figure()
plt.hist(output, bins=20, density=True)
plt.plot(np.linspace(-10, 20, 100), stats.laplace.pdf(np.linspace(-10, 20, 100), 5, scale=2))
Plot
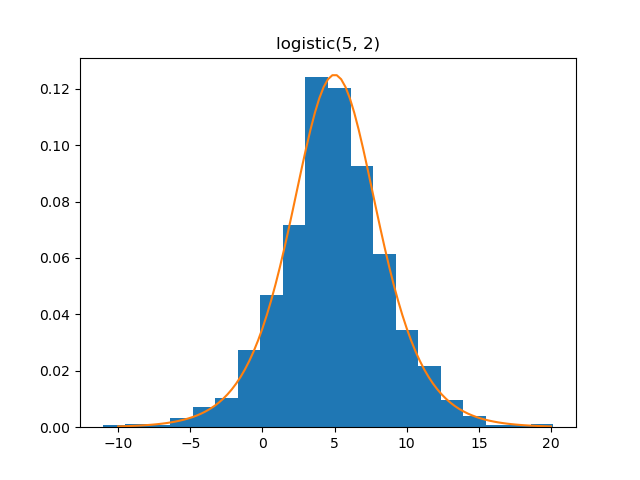
Logistic
Demo
from pydpm._sampler import Basic_Sampler
import scipy.stats as stats
output = sampler.logistic(np.ones(1000)*5, np.ones(1000)*2)
plt.figure()
plt.hist(output, bins=20, density=True)
plt.plot(np.linspace(-10, 20, 100), stats.logistic.pdf(np.linspace(-10, 20, 100), 5, scale=2))
Plot
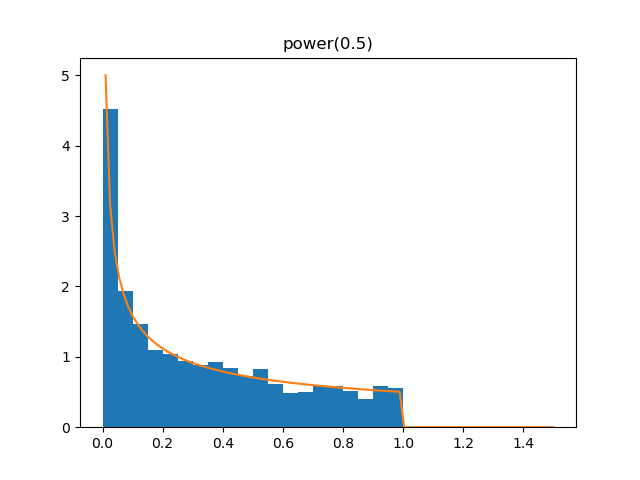
Power
Demo
from pydpm._sampler import Basic_Sampler
import scipy.stats as stats
output = sampler.power(np.ones(1000)*0.5)
plt.figure()
plt.hist(output, bins=20, density=True)
plt.plot(np.linspace(0, 1.5, 100), stats.powerlaw.pdf(np.linspace(0, 1.5, 100), 0.5))
Plot
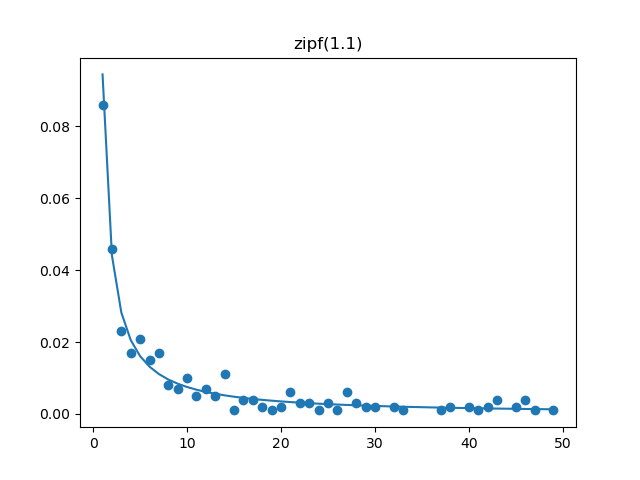
Zipf
Demo
from pydpm._sampler import Basic_Sampler
import scipy.stats as stats
output = sampler.zipf(np.ones(1000)*1.1)
counter = Counter(output)
filter = np.array([[key, counter[key]] for key in counter.keys() if key < 50])
plt.figure()
plt.scatter(filter[:, 0], filter[:, 1] / 1000)
plt.plot(np.arange(1, 50), stats.zipf(1.1).pmf(np.arange(1, 50)))
Plot
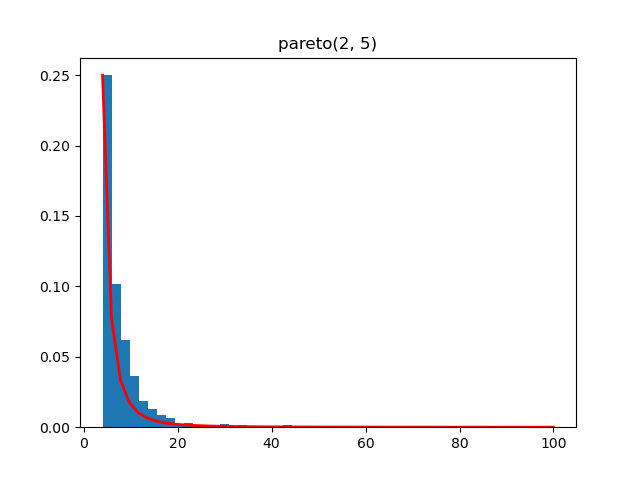
Pareto
Demo
from pydpm._sampler import Basic_Sampler
import scipy.stats as stats
output = sampler.pareto(np.ones(1000) * 2, np.ones(1000) * 5)
plt.figure()
count, bins, _ = plt.hist(output, bins=50, density=True, range=(np.min(output), 100))
a, m = 2., 5. # shape and mode
fit = a * m ** a / bins ** (a + 1)
plt.plot(bins, max(count) * fit / max(fit), linewidth=2, color='r')
plt.title('pareto(2, 5)')
plt.show()
Plot
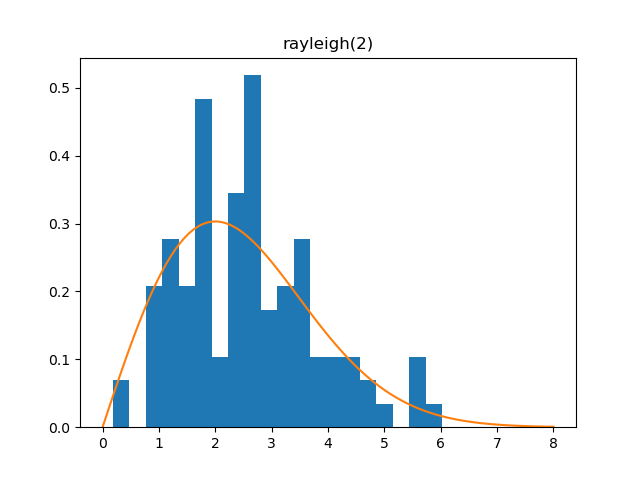
Rayleigh
Demo
from pydpm._sampler import Basic_Sampler
import scipy.stats as stats
output = sampler.rayleigh(np.ones(1000)*2.0)
plt.figure()
plt.hist(output, bins=20, density=True)
plt.plot(np.linspace(0, 8, 100), stats.rayleigh(scale=2).pdf(np.linspace(0, 8, 100)))
Plot
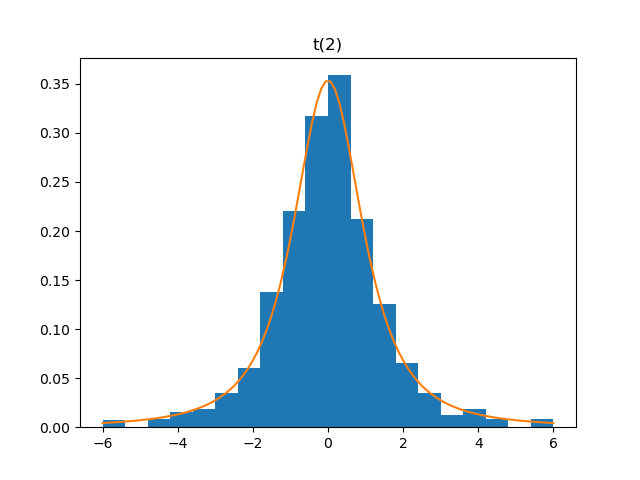
T
Demo
from pydpm._sampler import Basic_Sampler
import scipy.stats as stats
output = sampler.t(np.ones(1000)*2.0)
plt.figure()
plt.hist(output, bins=20, density=True, range=(-6, 6))
plt.plot(np.linspace(-6, 6, 100), stats.t(2).pdf(np.linspace(-6, 6, 100)))
Plot
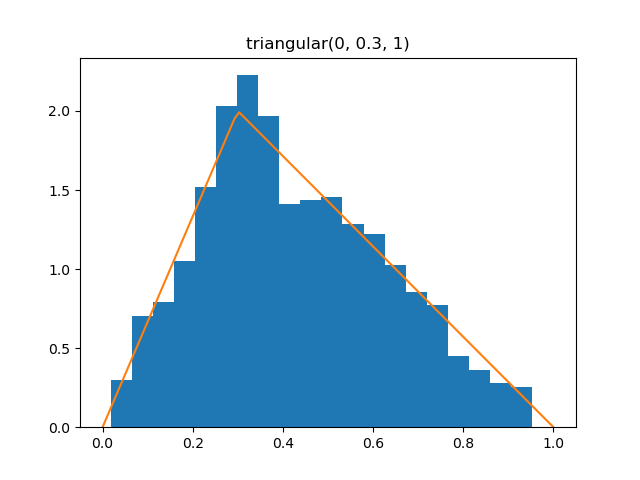
Triangular
Demo
from pydpm._sampler import Basic_Sampler
import scipy.stats as stats
output = sampler.triangular(np.ones(1000)*0.0, 0.3, 1)
plt.figure()
plt.hist(output, bins=20, density=True)
plt.plot(np.linspace(0, 1, 100), stats.triang.pdf(np.linspace(0, 1, 100), 0.3))
Plot
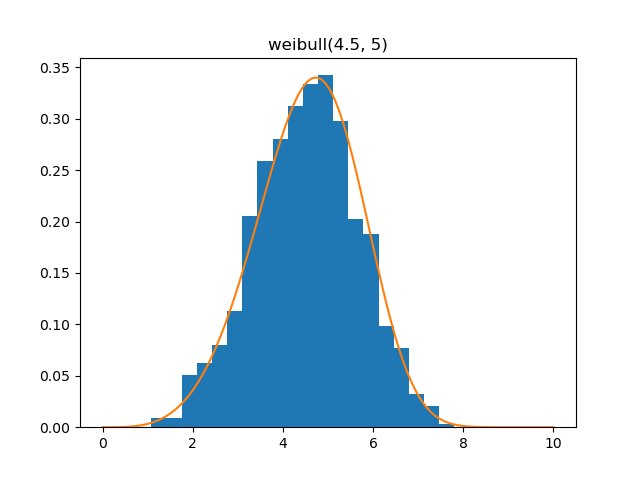
Weibull
Demo
from pydpm._sampler import Basic_Sampler
import scipy.stats as stats
output = sampler.weibull(np.ones(1000)*4.5, 5)
plt.figure()
plt.hist(output, bins=20, density=True)
plt.plot(np.linspace(0, 10, 100), stats.weibull_min.pdf(np.linspace(0, 10, 100), 4.5, scale=5))
Plot